Unit Conversions
There are situations in every day life where we must convert from one unit to another. If a recipe calls for 250 grams of cheese, how many pounds should you buy from the grocery store? How many tablespoons are in a 1/8 cup? Which is a better deal: A pint of orange juice for $1.00 or 500 mL of orange juice for $1.00?
To convert from one unit to another, we need to know how units are related to each other. These relationships are often given as an equation which each side being equivalent to the other, but with different units. We have seen some examples previously in this chapter, such as:
1 kg = 2.2 lb
1 kg = 1,000 g
1 mL = 0.001 L
1 cup = 16 Tbsp
In this section, we will use these types of equations as unit conversion factors and convert from one unit to another.
Unit Conversion Factors
If you have observed a meter stick, you will have noticed that 1 meter (m) is the same length as 100 centimeters (cm). There are 100 cm in 1 m, and we can write this relationship as follows:
100 cm = 1 m
Suppose we divide both sides of the equation by 1 m (both the number and the unit):
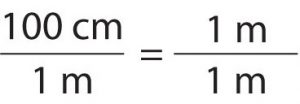
As long as we perform the same operation on both sides of the equals sign, the expression remains an equality. Look at the right side of the equation; it now has the same quantity in the numerator (the top) as it has in the denominator (the bottom). Any fraction that has the same quantity in the numerator and the denominator has a value of 1:
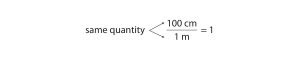
We know that 100 cm is 1 m, so we have the same quantity on the top and the bottom of our fraction, although it is expressed in different units. A fraction that has equivalent quantities in the numerator and the denominator but expressed in different units is called a unit conversion factor.
Here is a simple example. How many centimeters are there in 3.55 m? Perhaps you can determine the answer in your head. If there are 100 cm in every meter, then 3.55 m equals 355 cm. To solve the problem more formally with a unit conversion factor, we first write the quantity we are given, 3.55 m. Then we multiply this quantity by a unit conversion factor, which is the same as multiplying it by 1. We can write 1 as
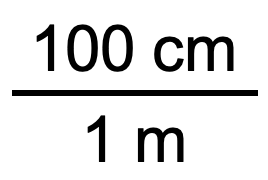
and multiply:
![An equation that reads as follows: [(3.55 m) / 1] x [(100 cm) / (1 m)]](https://mhcc.pressbooks.pub/app/uploads/sites/35/2021/10/Screen-Shot-2021-10-28-at-10.24.31-AM-300x87.png)
The 3.55 m can be thought of as a fraction with a 1 in the denominator. Because m, the abbreviation for meters, occurs in both the numerator and the denominator of our expression, they cancel out:
![An equation that reads as follows: [(3.55 m) / 1] x [(100 cm) / (1 m)]. The "m" units are crossed out.](https://mhcc.pressbooks.pub/app/uploads/sites/35/2021/10/Screen-Shot-2021-10-28-at-10.29.46-AM-300x87.png)
The final step is to perform the calculation that remains once the units have been canceled:
![An equation that reads as follows: [3.55 / 1] x [(100 cm) / 1] = 3.55 x 100 cm = 355 cm](https://mhcc.pressbooks.pub/app/uploads/sites/35/2021/10/Screen-Shot-2021-10-28-at-10.33.21-AM-300x38.png)
In the final answer, we omit the 1 in the denominator. Thus, by a more formal procedure, we find that 3.55 m equals 355 cm. A generalized description of this process is as follows:
quantity (in old units) × unit conversion factor = quantity (in new units)
You may be wondering why we use a seemingly complicated procedure for a straightforward conversion. In later studies, the conversion problems you will encounter will not always be so simple. If you can master the technique of applying unit conversion factors, you will be able to solve a large variety of problems.
In the previous example, we used the fraction
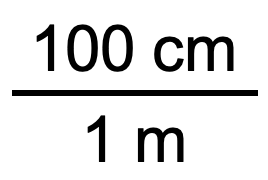
as a unit conversion factor. Does the unit conversion factor
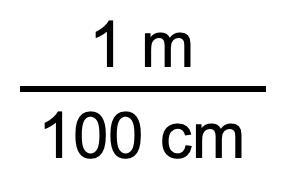
also equal 1? Yes, it does; it has the same quantity in the numerator as in the denominator (except that they are expressed in different units). Why did we not use that unit conversion factor? If we had used the second unit conversion factor, the original unit would not have canceled, and the result would have been meaningless. Here is what we would have gotten:
![An equation that reads as follows: [(3.55 m)/1]x[(1 m)/(100 cm)]=(3.55xmx1xm)/(1x100xcm)=(3.55xm^2)/(11xcm)](https://mhcc.pressbooks.pub/app/uploads/sites/35/2021/10/Screen-Shot-2021-10-28-at-10.44.34-AM-300x36.png)
For the answer to be meaningful, we have to construct the unit conversion factor in a form that causes the original unit to cancel out. The following figure shows a concept map for constructing a proper conversion.
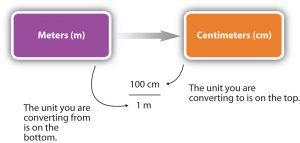
Unit Conversion Example 1
If a recipe calls for 250 grams (g) of cheese, how many pounds (lb) should you buy from the grocery store? (454 g = 1 lb)
Solution
We start with what we are given, 250 g. We want to change the unit from g to lb. There are 454 g in 1 lb. From this relationship, we can construct two unit conversion factors:
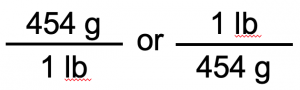
We use the unit conversion factor that will cancel out the original unit, g, and introduce the unit we are converting to, which is lb. The unit conversion factor that does this is the one on the right:
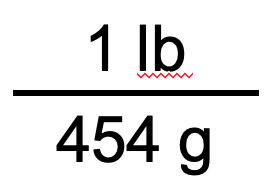
Now that we have our unit conversion factor picked out, we can use our general equation:
quantity (in old units) × unit conversion factor = quantity (in new units)
![An equation that reads as follows: [(250g)/1]x[(1lb)/(454g)]=(250xgx1xlb)/(1x454xg)=(250xlb)/454=0.55 lb](https://mhcc.pressbooks.pub/app/uploads/sites/35/2021/10/Screen-Shot-2021-10-28-at-11.09.05-AM-300x34.png)
The final answer is 0.55 lb.
Unit Conversion Example 2
A salad dressing recipe that calls for 1/4 cup of olive oil is cut in half to decreases the number of servings prepared from 8 to 4. To make half of the recipe, 1/8 cup of olive oil is needed. Most kitchens do not have a 1/8 cup measuring vessel, however, a tablespoon is more common. How many tablespoons (Tbsp) are in a 1/8 cup (c)? (1 cup = 16 Tbsp)
Solution
We start with what we are given, 1/8 cup. We want to change the unit from cup to Tbsp. There are 16 Tbsp in 1 cup. (1 cup = 16 Tbsp) From this relationship, we can construct two unit conversion factors:
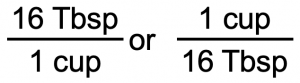
We use the unit conversion factor that will cancel out the original unit, cup, and introduce the unit we are converting to, which is Tbsp. The unit conversion factor that does this is the one on the left:
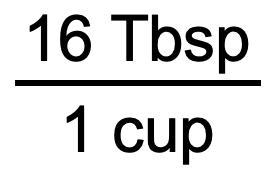
Now that we have our unit conversion factor picked out, we can use our general equation:
quantity (in old units) × unit conversion factor = quantity (in new units)
![An equation that reads as follows: [(0.125cup)/1]x[(16Tbsp)/(1cup)]=(0.125xcupx16xTbsp)/(1x1xcup)=(0.125x16xTbsp)/1=2Tbsp](https://mhcc.pressbooks.pub/app/uploads/sites/35/2021/11/Screen-Shot-2021-11-02-at-8.30.52-PM-300x30.png)
The final answer is 2 Tbsp.
Using Density as a Unit Conversion Factor
Density can be used to convert between the mass and the volume of a substance. Consider sugar, which has a density of 1.6 g/mL. The density tells us that 1.6 g of sugar has a volume of 1 mL. We can write that relationship as follows:
1.6 g sugar = 1 mL sugar
This relationship can be used to construct two unit conversion factors:
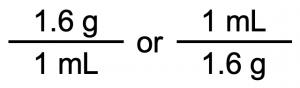
Which one do we use? It depends, as usual, on the units we need to cancel and introduce. For example, suppose we want to know the mass in grams of 250 mL of sugar (perhaps we have a mass balance that measures grams, but no measuring cups for milliliters). We would use the unit conversion factor that has milliliters on the bottom (so that the milliliter unit cancels) and grams on top so that our final answer has a unit of mass:
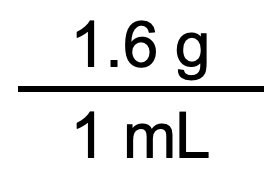
Now we can use this unit conversion factor in the same procedure described earlier:
quantity (in old units) × unit conversion factor = quantity (in new units)
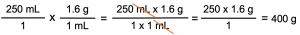
The final answer is 400 g of sugar.
Unit Conversion with Density Example
A recipe calls for 500 g of milk, but you have no mass balance to weight out ingredients in grams. However, you do have a cup that measures milliliters (mL) of liquid ingredients. What is the volume in mL of 500 g of milk? The density of milk is 1.03 g/mL.
Solution
The density 1.03 g/mL can be used as a unit conversion factor (1.03 g = 1 mL). There are two possible ways to write the unit conversion factor:
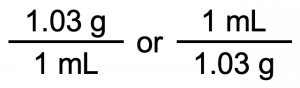
We want to cancel out g, so g should be on the bottom. Also, we want to convert to mL, so mL should be on the top. Thus, we need to use the unit conversion factor on the right:
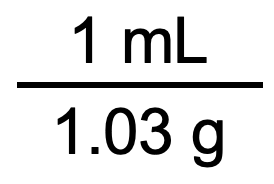
We can now follow our general procedure for unit conversions:
quantity (in old units) × unit conversion factor = quantity (in new units)
![An equation that reads as follows: [(500g)/(1)]x[(1mL)/(1.03g)]=(500xgx1xmL)/(1x1.03xg)=(500x1xmL)/(1x1.03)=485mL](https://mhcc.pressbooks.pub/app/uploads/sites/35/2021/11/Screen-Shot-2021-11-02-at-9.18.41-PM-300x33.png)
The final answer is 485 mL of milk.
Attributions
This page is based on “Chemistry 2e” by Paul Flowers, Klaus Theopold, Richard Langley, William R. Robinson, PhD, Openstax which is licensed under CC BY 4.0. Access for free at https://openstax.org/books/chemistry-2e/pages/1-introduction
This page is based on “Chemistry of Cooking” by Sorangel Rodriguez-Velazquez which is licensed under CC BY-NC-SA 4.0. Access for free at http://chemofcooking.openbooks.wpengine.com/
This page is based on “The Basics of General, Organic, and Biological Chemistry” by David W Ball, John W Hill, Rhonda J Scott, Saylor which is licensed under CC BY-NC-SA 4.0. Access for free at http://saylordotorg.github.io/text_the-basics-of-general-organic-and-biological-chemistry/index.html

