The naturally occurring monosaccharides contain three to seven carbon atoms per molecule. The simplest sugars are glyceraldehyde and dihydroxyacetone, shown in part (a) of the figure below. Notice that two structures are shown for glyceraldehyde. These structures are stereoisomers, molecules having the same structural formula but differing in the arrangement of atoms or groups of atoms in three-dimensional space. If you make models of the two stereoisomers of glyceraldehyde, you will find that you cannot place one model on top of the other and have each functional group point in the same direction. However, if you place one of the models in front of a mirror, the image in the mirror will be identical to the second stereoisomer in part (b) of the figure below. Molecules that are nonsuperimposable (nonidentical) mirror images of each other are a type of stereoisomer called enantiomers (Greek enantios, meaning “opposite”).

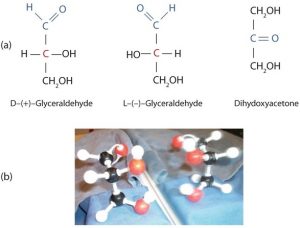
A key characteristic of enantiomers is that they have a carbon atom to which four different groups are attached. Note, for example, the four different groups attached to the central carbon atom of glyceraldehyde (part (a) of the figure above). A carbon atom that has four different groups attached is a chiral carbon. If a molecule contains one or more chiral carbons, it is likely to exist as two or more stereoisomers. Dihydroxyacetone does not contain a chiral carbon (it does not have a carbon atom that has four different groups attached to itself) and thus does not exist as a pair of stereoisomers. Glyceraldehyde, however, has a chiral carbon and exists as a pair of enantiomers. Except for the direction in which each enantiomer rotates plane-polarized light, these two molecules have identical physical properties. D-glyceraldehyde rotates plane-polarized light in the clockwise direction. L-glyceraldehyde rotates plane-polarized light in the counterclockwise direction.

The two enantiomers of glyceraldehyde are especially important because monosaccharides with more than three carbon atoms can be considered as being derived from them. Thus, D-glyceraldehyde and L-glyceraldehyde provide reference points for designating and drawing all other monosaccharides. Sugars whose Fischer projections terminate in the same configuration as D-glyceraldehyde are designated as D sugars; those derived from L-glyceraldehyde are designated as L sugars.

Note

By convention, the penultimate (next-to-last) carbon atom has been chosen as the carbon atom that determines if a sugar is D or L. It is the chiral carbon closest to the bottom of the structure as written.

Special Section: Polarized Light

A beam of ordinary light can be pictured as a bundle of waves; some move up and down, some sideways, and others at all other conceivable angles. When a beam of light has been polarized, however, the waves in the bundle all vibrate in a single plane. Light altered in this way is called plane-polarized light. Much of what chemists know about stereoisomers comes from studying the effects they have on plane-polarized light. In this illustration, the light on the left is not polarized, while that on the right is polarized.

Sunlight, in general, is not polarized; light from an ordinary light bulb or an ordinary flashlight is not polarized. One way to polarize ordinary light is to pass it through Polaroid sheets, special plastic sheets containing carefully oriented organic compounds that permit only light vibrating in a single plane to pass through. To the eye, polarized light doesn’t “look” any different from nonpolarized light. We can detect polarized light, however, by using a second sheet of polarizing material, as shown here.

Certain substances act on polarized light by rotating the plane of vibration. Such substances are said to be optically active. The extent of optical activity is measured by a polarimeter, an instrument that contains two polarizing lenses separated by a sample tube, as shown in the accompanying figure. With the sample tube empty, maximum light reaches the observer’s eye when the two lenses are aligned so that both pass light vibrating in the same plane. When an optically active substance is placed in the sample tube, that substance rotates the plane of polarization of the light passing through it, so that the polarized light emerging from the sample tube is vibrating in a different direction than when it entered the tube. To see the maximum amount of light when the sample is in place, the observer must rotate one lens to accommodate the change in the plane of polarization.

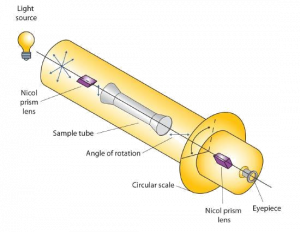
Some optically active substances rotate the plane of polarized light to the right (clockwise) from the observer’s point of view. These compounds are said to be dextrorotatory; substances that rotate light to the left (counterclockwise) are levorotatory. To denote the direction of rotation, a positive sign (+) is given to dextrorotatory substances (such as D-(+)-glyceraldehyde), and a negative sign (−) is given to levorotatory substances (such as L-(−)-glyceraldehyde).

Cyclic Structures of Monosaccharides

So far we have represented monosaccharides as linear molecules, but many of them also adopt cyclic structures. The conversion from linear to cyclic structure occurs because of the monosaccharides ability to react with itself. In the case of D-glucose shown below, the OH group on the fifth carbon atom reacts with the first carbon atom to form a ring of five carbons and one oxygen. Cyclic structures with rings consisting of five or six atoms are the most stable.

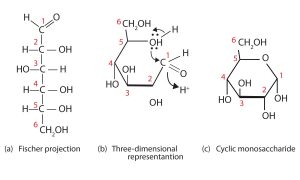
When a straight-chain monosaccharide forms a cyclic structure, the carbonyl oxygen atom may be pushed either up or down, giving rise to two stereoisomers, as shown in the figure below. The structure shown on the left side of the figure below, with the OH group on the first carbon atom projected downward, represent what is called the alpha (α) form. The structures on the right side, with the OH group on the first carbon atom pointed upward, is the beta (β) form.

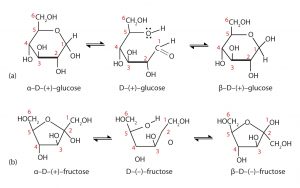
It is possible to obtain a sample of crystalline glucose in which all the molecules have the α structure or all have the β structure. The α form melts at 146°C and rotates plane-polarized light to an angle of +112°, while the β form melts at 150°C and rotates plane-polarized light to an angle of +18.7°. The differences in physical properties are a result of the different structures of these isomers. When the sample is dissolved in water, however, a mixture is soon produced containing both isomers as well as the straight-chain form, in dynamic equilibrium (shown in part (a) of the figure above). You can start with a pure crystalline sample of glucose consisting entirely of either isomer, but as soon as the molecules dissolve in water, they open to form the straigh-chain form and then reclose to form either the α or the β isomer. The opening and closing repeats continuously in an ongoing interconversion between isomers and is referred to as mutarotation (Latin mutare, meaning “to change”). At equilibrium, the mixture consists of about 36% α-D-glucose, 64% β-D-glucose, and less than 0.02% of the open-chain aldehyde form. The observed rotation of plane-polarized light for this solution is +52.7°.

In the figures above and elsewhere in this book, the cyclic forms of sugars are depicted using a convention first suggested by Walter N. Haworth, an English chemist. The molecules are drawn as planar hexagons with a darkened edge representing the side facing toward the viewer. The structure is simplified to show only the oxygen atoms or OH groups attached to the carbon atoms. Any group written to the right in a Fischer projection appears below the plane of the ring in a Haworth projection, and any group written to the left in a Fischer projection appears above the plane in a Haworth projection.

The difference between the α and the β forms of sugars may seem trivial, but such structural differences are often crucial in biochemical reactions. This explains why we can get energy from the starch in potatoes and other plants but not from cellulose, even though both starch and cellulose are polysaccharides composed of glucose molecules linked together. We will examine the effects of these differences more closely in the section titled “Polysaccharides.”

Attributions

This page is based on “Chemistry 2e” by Paul Flowers, Klaus Theopold, Richard Langley, William R. Robinson, PhD, Openstax which is licensed under CC BY 4.0. Access for free at https://openstax.org/books/chemistry-2e/pages/1-introduction

This page is based on “The Basics of General, Organic, and Biological Chemistry” by David W Ball, John W Hill, Rhonda J Scott, Saylor which is licensed under CC BY-NC-SA 4.0. Access for free at http://saylordotorg.github.io/text_the-basics-of-general-organic-and-biological-chemistry/index.html