Lesson 5: Geometry II–Triangles and Circles
Word List
| 1. adjacent | next to, near. The adjacent side and the hypotenuse form the two sides of an angle of a right triangle.
Example: The Fire Station is adjacent to City Hall. |
| 2. to draw | to make lines with a pencil.
Example: He drew a line from the center of the circle to the outside edge. Related words: drawn, drawing. |
| 3. figure | closed shapes drawn to show two dimensions (plane figures) or three dimensions (solid figures).
Example: This three-sided figure is a triangle. |
| 4. formula | a set of numbers and letters that state a general mathematical truth.
Example: The formula for the area of a rectangle is |
| 5. hypotenuse | the side of a right triangle opposite the right angle.
Example: The hypotenuse, for this triangle, measures 7.093″ in length. |
| 6. opposite | not next to, but across from.
Example: The opposite side of a right triangle is the side across from the angle formed by the hypotenuse and the adjacent side. |
| 7. pi (a letter) | a Greek letter given the value of 3.14 which is the number of times that the length of the diameter will divide into the circumference.
Example: Multiply x times the diameter to get the length of the circumference. |
| 8. point | a point has location, but no size.
Example: This point is 5.3″ from the center of the circle, but it doesn’t have length nor width. |
| 9. plane | a space with two dimensions (length and width).
Example: A plane is a flat surface with length and width but no depth. |
| 10. plane geometry | a part of mathematics that studies plane figures like squares, circles, and triangles.
Example: Plane geometry teaches us about figures with the two dimensions of length and width.
|
| 11. solid geometry | a part of mathematics that studies solid figures like cubes, spheres, and pyramids.
Example: We can learn about figures with the three dimensions of length, width and height in the study of solid geometry. |
| 12. solution | the process of getting an answer to a problem; also the answer at the end of the process.
Example: The correct solution to C= d x π, where d = 7 in. is 22 in. |
| 13. to round off | to give a number in even units, instead of exactly.
Example: When you round off 697, you say “about 700”. |
| 14. term | a word or phrase which has a limited, special meaning in some science or art.
Example: “Hypotenuse” is a special term found in geometry. |
| 15. trigonometry | the branch of mathematics that studies the angles and sides of right triangles.
Example: The machinist must learn a few things from trigonometry. |
Definitions and Practice
GEOMETRY, Part II: Triangles and Circles
Machinists will also need some knowledge of triangles and circles, their properties, and how to measure them.
A.) TRIANGLES:
- Plane Figures:
- The kind of geometry we are studying now is plane geometry, i.e. the geometry that studies figures (closed shapes) which lie in a plane (a two-dimensional space). Examples of plane figures are square, rectangle, circle and triangle. There is also another kind of geometry called solid geometry which studies solids (three dimen sions), like cubes, spheres, and pyramids. We will not study them.
- About Triangles:
- A triangle is a plane figure which has three straight sides and three angles.
- The three angles of a triangle always total 180°, i.e., when you add the degrees of each of the three angles together, you will always get a total of 180°.
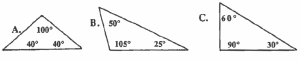
In triangle A, the three angles add up to 180°. (40° + 100° + 40° = 180°)
In triangle B, the three angles add up to 180°. (50° + 105° + 25° = 180°)
In triangle C, the three angles add up to 180°. (90° + 60° + 30° = 180°)
3. Right Triangles
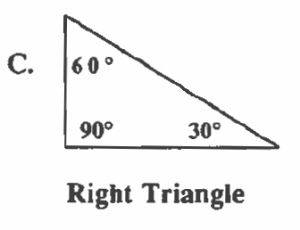
A triangle that contains a right angle, like triangle C, is called a right triangle. One of the angles is equal to 90° and the other two angles add up to 90° ; they are complementary angles.
A right triangle has some special names for its sides:
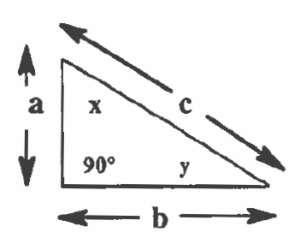
The side opposite the 90° angle (c) is called the hypotenuse.
Side a and side b are called the other two sides.
If we look at angle y, then side a is the side opposite from angle y, and side b is the side adjacent to angle y. Side c is always the hypotenuse.
If we look at angle x, then side b is the opposite side, and side a is the adjacent side. Side c is, again, the hypotenuse.
The terms hypotenuse, opposite side, and adjacent side will be important, when we study trigonometry in a later lesson. Trigonometry is the branch of mathematics that studies the angles and sides of right triangles; trigonometry is very useful to scientists and to many practical trades like engineering and machine shop work.
Comprehension Questions

Calculations for the third angle
Examples: We know that the three angles of a triangle always equal 180°. If we know two of the angles, we can figure out the third angle by adding the first two and subtracting the total from 180°; e.g.,
- A triangle has two angles equal to 14° and 35°. How many degrees are in the third angle?
-
- Step I: Add the two angles; 14° + 35° = 49°
- Step 2: Subtract from 180°; 180 – 49° = 137°.
- A right triangle has one angle equal to 47°. How many degrees are in the third angle?
-
- Step 1: Add the angle to 90°; 47° + 90° = 137°
- Step 2: Subtract from 180°; 180° – 137° = 43°.
Find the number of degrees in the third angle
B.) CIRCLES:
1. Important Terms
It is important to learn the mathematical terms (words) that are used to talk about circles.
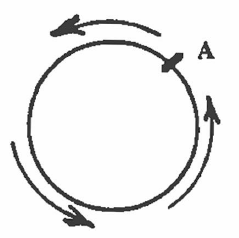 |
The distance around the outside edge of the circle is called the circumference. In the picture, the distance from point A around the circle back to point A–that distance is the circumference. |
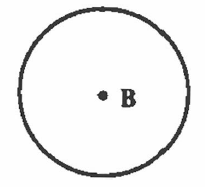 |
Each circle has a center point (B). All the points on the circumference are of equal distance from the center. |
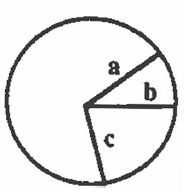 |
A straight line drawn from the center to the circumference is called a radius. The plural of radius is radii (pronounced ray-dee-eye). There can be as many radii as you wish to draw; all are equal to each other. In the picture, a, b, and c are radii; a = b = c. |
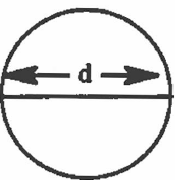 |
A straight line drawn through the center and touching both sides of the circumference is called a diameter. A diameter must go through the center of the circle. A diameter is equal to two radii: d = 2r. |
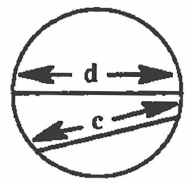 |
A straight line drawn through the circle and touching both sides, but not passing through the center, is called a chord. In the picture, d = diameter and c = chord. |
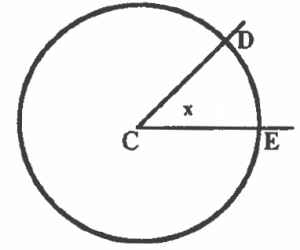 |
The angle DCE cuts the circumference at points D and E. The part of the circumference inside the arms of the angle is called an arc (a part of the circle’s circumference ). We write the arc DE like this:
It is read “arc DE”. |
2. Pi (π) and its use
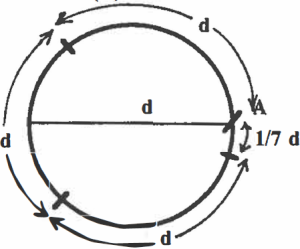
The length of the diameter of any circle can be divided into the circumference of that same circle. It will go in approximately 3 1/7 times. In decimal form C + d = 3.1416. This number is given a special name, pi, and a special symbol 1t which stands for the number 3 1/7 or 3.1416. (These values of 1t are only approximations; your scientific calculator gives a value of 3.1415927; even this value is still approximate; the value of 1t has been calculated out to hundreds of decimal places and there is no exact value. but 3.1416 and 3.1415927 are close enough.
One use for π is to find the length of the circumference of a circle. If you know the length of the diameter of the circle, you can multiply that length by 1t and get the length of the circle. We can write down this relationship in a general statement called a mathematical formula; this formula will be true for all circles with any length diameter.
Formula: C = dπ
(This is read, “The circumference is equal to the diameter times π.”)
For example, what is the circumference of a circle which has a diameter of 35 inches?
Solution: C = dπ; put in the values: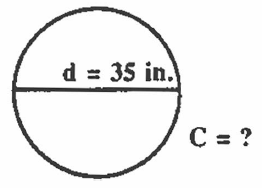
C = 35 x 3 1/7
C = 35/1 x 22/7 convert to improper fractions
C = 5 x 22 reduce fractions with cross multiples
C = 110 in.
Practice with Circles
USING THE SCIENTIFIC CALCULATOR TO FIND CIRCUMFERENCE:
The third key in the bottom row of black keys says: When you press it, you will get the value of π, which is 3.1415927 on this calculator.
Example: Find the circumference of a circle with d = 2.5 in. Round off the answer to the nearest thousandth.
Solution: 2.5 x π = 7.8539816 = 7.854 in. (rounding off).
Steps:
1) Turn the calculator on.
2) Enter 2.5
3) Press x (multiply)
4) Press π key.
5) Press = (answer appears on display).
Calculator Practice

