Lesson 4: Geometry–Angles and Their Measurement

WORD LIST

1.) point	a word from geometry, used to show a definite position, but which has no size, shape or length. Example: Draw a line from Point A to Point B.
2.) surface	a word from geometry, used to talk about something which has length and width, but no thickness; it has only two dimensions. Example: How many square inches are in the top surface of that part?
3.) solid	a word from geometry, used to talk about something which has length, width, and height; it has three dimensions. Example: A cube has six sides; it is a solid with length, width, and height all equal.
4.) property	a principal quality which something has. Example: All right angles have the property of being equal to 90°
5.) to discuss	to talk about something with another person. Example: Let’s discuss the dimensions and tolerances on this blue­print.
6.) to originate	to begin at a particular place; to begin at a point and reach out from there. Example: The two sides of an angle originate at a common point.
7.) right angle	an angle equal to 90°. Example: An angle of 90° is called a right angle.
8.) perpendicular to	two lines are perpendicular to each other when they form an angle of 90°. Example: The wall is perpendicular to the floor.
9.) to rotate	to tum in a circular path around a center point or around an axis (center line). 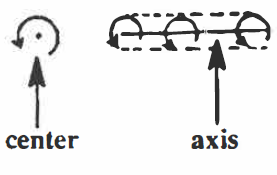Example: The earth rotates around the sun.
10.) angle	the shape made by two straight lines that meet at a point. Example: Carlos measured the angle very carefully.
11.) degree	a unit of measure for angles. A degree is 1/360 part of the edge of a circle. Example: There are 360 degrees in a circle.
12.) minute	1/60 of a degree; one degree= 60 minutes. Example: How many minutes are in a degree? There are 60.
13.)  second	1/60 of a minute; one minute = 60 seconds; one degree= 3600 seconds. Example: One minute contains 60 seconds.
14.) to borrow	to take units from a neighboring, larger unit to increase the amount from which another amount will be subtract­ed. Example: In arithmetic borrowing is done in units of ten; for angles we borrow in units of 60.
15.) vertex	the point at which the two straight lines of an angle meet. Example: The two sides of the angle meet at the vertex.

GEOMETRY:    Angles and Their Measurement

Geometry is a part of mathematics that deals with points, lines, surfaces, and solids, along with their properties and their measurement. Machinists will need some knowledge of geometry, when they read blueprints, make parts, and discuss the work of the machine shop.

A.  ANGLES:

1.  Angle Information:

• An angle is the space between two straight lines which are drawn from the same point.
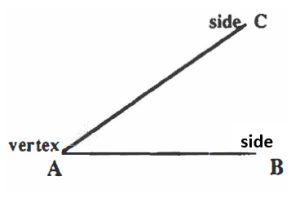
• The two lines are called the sides.
• The common point is called the vertex.
• In the picture the vertex is named A; the end of one side is called B; and the end of the other side is called C.
• The sides of the angle are AB and AC.
• The angle formed by the sides is called angle CAB or BAC. (When naming an angle, give the letter for an end of one of the sides, give the letter for the vertex, and then the letter for the end of the other side.)
• This sign can be used as an abbreviation for the word angle: ∠
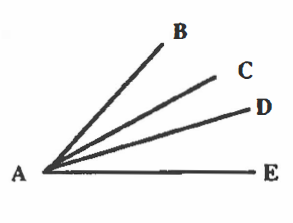
  And so angle CAB can be shown by∠CAB.
• More than one angle can originate from the vertex. In the second picture, ∠s BAC, CAD, and DAE all have the same vertex at point A.

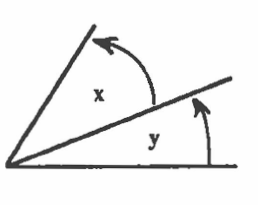
• Another way to name an angle is to use small letters placed between the two sides, near a part of a circle with an arrowhead. In the picture, the angles are x and y.

B. Angle Measurement:

1. Degrees:

• The size of an angle is measured by how far one of the sides has moved away from the other. The unit of measure is degrees. When one of the sides is lying on top of the other, then the size of the angle is 0°.
• As one side moves away from the other, the angle opens up and the number of degrees increases. When one of the sides is perfectly horizontal and the other side is perfectly vertical, they form a right angle, which is 90 °. In the picture, we can say that the line CD is perpendicular to line AB.
  
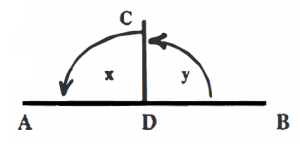
  We mean that ∠x is equal to ∠y. Both x and y are equal to 90°. Angles can be added together, so we know that the straight line ADB is equal to 180°.Therefore we know these things to be true:
  • When two right angles are added together, they form a straight line.
  • A right angle = 90°.
  • A straight line = 180° = two right angles.
• If the side continues to rotate on the vertex, it opens up a larger and larger angle which will reach 270° and finally comes back to where it started. This is a trip of one complete circle, which is equal to 360°.

• A degree can be divided into smaller units called minutes; there are 60 minutes in one degree. The abbreviation for minute is the same as for feet: ‘. An angle of 44° 23′ would be read “44 degrees and 23 minutes”; it is the same as 44 23/60 degrees.
• Each minute can also be divided further into 60 smaller units which are called seconds and which are shown by the abbreviation which we also use to show inches: “. An angle of 35° 12′ 36″ is 35 degrees, 12 minutes and 36 seconds wide. A second is 1/60 of a minute; a second 1/3600 of a degree.

Adding and Subtracting Angles

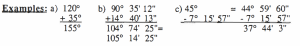
Comments on examples a, b, and c above.

a) Angles can be added or subtracted.

b) When adding produces more than 60′ or 60″, the 60′ or the 60″ are changed into the larger unit; e.g., 89′ = 1 ° 29′. (There are 60′ in one degree, plus 29′ left over.)

c) When subtracting, it may be necessary to borrow;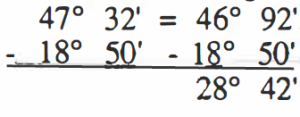

e.g., Take 1° from 47°, leaving 46°, change the 1° into 60′, and add the 60′ to the 32′ that are already there. Now we can subtract.

ADDITIONAL  INFORMATION:

•  Two angles, which equal 90° when added, are called complementary angles. For example, here are some com­ plementary angles: 56° and 34° are complementary angles, because their swn is equal to 90°; the same for 71° and 19°.
• One complementary angle is said to be the complement of the other angle, e.g. 25° is the complement of 65°. To find what the complement of an angle is, subtract the angle from 90° in order to figure out the complement.For example, what is the complement of 42°?
  Solution: 90° – 42° = 48°. The complement of 42° is 48°. The angles 42° and 48° are complementary.
• Two angles, which equal 180° when added, are called supple­mentary angles, and one angle is said to be the supplement of the other.For example, 24° and 166° are supplementary angles. We can also say that 24° is the supplement of 166° , and 166° is thesupplement of 24°.To find what the supplement of an angle is, subtract the angle from 180°; e.g.   What is the supplement of 97°?
  Solution: 180° – 97° = 83° The supplement of an angle of 97 is 83°.

Some other Sample Problems: