Visualizing the Center

In math classes, it is easy to think about the center of a circle.  We have the whole circle.  When making parts, they will have curves and round angles which are only sections of circles and their circumferences.  The whole circle is not put together.  Blueprints show a lot of arcs without the whole circle. Figure 1 shows a basic arc.

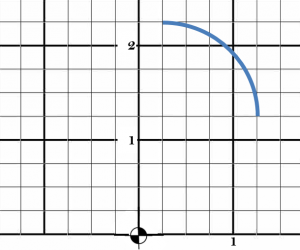
With the coordinate system, the two endpoints of the arc can be identified.

Maybe it is hard to ‘see’ the whole circle.  Let’s take a look at Figure 2.

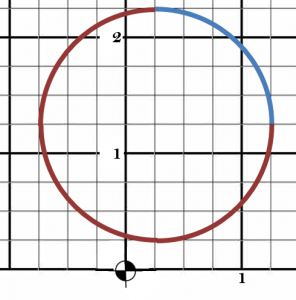
Is the center of the arc easier to think about?  Sure.

How can we identify the center’s coordinates?  Let’s see one way in Figure 3.

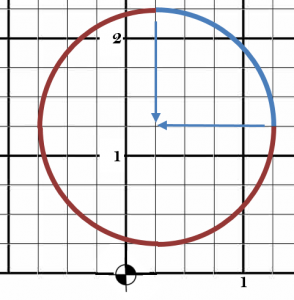
The start and end points of the arc will cross at the center.  Their arrows form a 90º angle at the center point.   That makes sense.  Endpoints are part of a circle. And from geometry, we know that any point on the circumference of a circle will meet at the center. This distance is the measurement of the radius.  So, the dimension for a start or end point to the center is a measurement of the radius.  The start point to the center and the end point to the center will be equal distances because they are radii.

This radial measurement is identified by the CNC code as an I, J, or K letter.   The I-code will affect the X-axis. The J-code will affect the Y-axis. And, the K-code affects the Z-axis.