History

One of the most successful textbooks in history is Elements. Euclid of Alexandria wrote it about 300 years Before the Common Era (BCE). Euclid writes about geometry. Geometry is the mathematical study of shapes.  It is the first discussion of geometry in history. It has been one of the most influential books in history.

To understand shapes, learners must understand some basic concepts, which Euclid introduces in Elements.

Four terms to understand are line, point, plane, and space.

Line, Line Segment, and Ray

A line can be extended forever. A line is infinite.  In math, this type of line has arrow heads on both ends.

<——————————————————–>

Think about the sun. The light from the sun can appear as lines. These lines start at the sun and go on forever in the other direction.   This is the definition of a ray.  A ray is a line with a starting point and goes to infinity in the other direction.

Ray is the root word for radiate.

For example:

The sun radiates heat and light to earth.  It takes eight minutes and 20 seconds (8:20) to reach our planet.

In math, geometry, and measurement, only a small part of line is used.  It is called a line segment or segment.  The line ends in both directions.

•——————————————————–•

Point

A point is the beginning or end of a line segment.

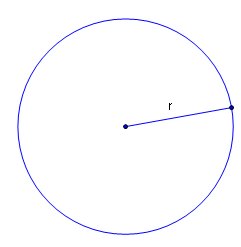
In the circle above, the center of the circle is the point where the line starts. The edge of the circle where the line stops is the point where the line ends.

Any two points can be joined by a straight line or line segment.

The Plane

If lines can go forever, then the place for those lines also goes on forever. The place for lines is called The Plane.

The Elements begins with plane geometry. In mathematics, the plane is a flat surface. It only has two measurements.  This is two-dimensional (2D) geometry or plane geometry. It is thought of as an infinitely vast (big, everywhere) and infinitely thin sheet that spreads across all of space. When working in 2D Euclidean space, the definite article is used, the plane, to refer to the whole space.

How do we draw shapes on a flat surface, for example, a piece of paper?

Euclid, in Elements, writes that exact shapes can be made with points on vertical and horizontal lines.

Vertical lines go up and down

It is clear that all the vertical lines go in the same up and down direction. They are parallel to each other.  Parallel means to go in the same direction without touching or crossing.

A couple of other ways to describe vertical lines are “up and down” or “x-axis”.

Horizontal Lines

In the picture to the left, we can see sand touching the clouds in the sky in the background. The straight line in nature is the horizon.

Lines that go in the direction of left and right are horizontal lines.

Horizontal lines go in a different direction—straight across. Horizontal lines are also parallel to one another.

Other ways to call the horizontal lines are “straight across” or “y-axis”.

Let’s try to describe the place or location of the vertical lines.

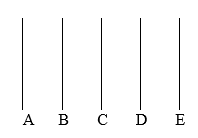
In the vertical lines above, there are five parallel vertical lines identified A-E. The lines are in different places in space. A is to the left of B, B is to the left of C, and so on. Line B is closest to line A, and line E is farthest away from line A. How can different vertical lines be located?

A horizontal line can solve the problem because horizontal lines run straight across. They go from side to side. See below.

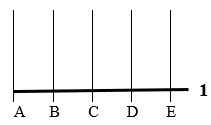
In the figure to the left, the horizontal line provides a reference line of 1 and clearly shows that vertical Lines A-E occur along different points on the bold horizontal line.

The addresses of the points can be identified as A1, B1, C1, and so on.

A piece of paper with vertical and horizontal lines is graph paper. Graph paper is an example of the plane that Euclid describes in Elements. Each place where a vertical line crosses (or intersects) a horizontal line is a point.

Combined vertical and horizontal lines can be called “The Plane”, a graph, graph paper, or 2-Dimensional (2D) space.

Many fundamental tasks in geometry, trigonometry, and graphing are performed in 2D space, or in other words, in the plane.

Space

The plane spreads across an area which is space. The horizontal and vertical lines extend across the plane and provide locations of points in space.  The Plane defines the borders of space in a geometry math problem.

This is the brilliance of Euclid’s book Elements. It provides the foundation about how to describe the location of something in space.

Cartesian Coordinates

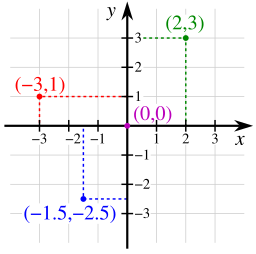
Cartesian means relating to the French mathematician and philosopher René Descartes , who, among other things, merges algebra and Euclidean geometry. The idea of the Cartesian coordinate system was developed in 1637 in two writings by Descartes.

In part two of his Discourse on Method, Descartes introduces the new idea of specifying the position of a point or object on a surface, using two intersecting axes as measuring guides. The second writing, La Géométrie, includes his application of algebra to geometry.

The study of geometry using the principles of algebra used to be called Cartesian Geometry. Today, it is called Analytic Geometry or Coordinate Geometry.

In mathematics, the Cartesian coordinate system determines a point in a plane through two numbers, called the x-coordinate and the y-coordinate. The two coordinates are defined by perpendicular directed lines called the the x-axis (abscissa) and the y-axis (ordinate). The unit length is designated on the two axes (see the chart to the right). Cartesian coordinate systems are also used in space (where three coordinates are used).

Here is an example of the infinity symbol drawn on The Plane.

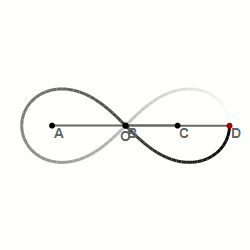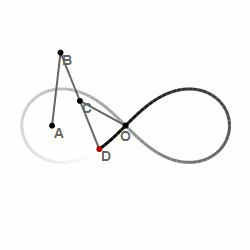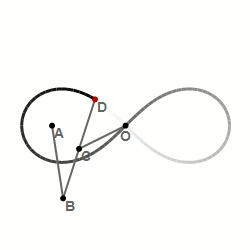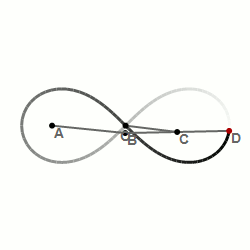
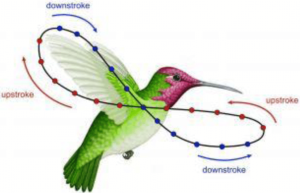
We can see that straight lines are able to create curves and round shapes on a flat surface (The Plane).  In infinity symbols means that something goes on forever without an and. It looks like the number eight on its side.  This pattern also appears in nature. The pattern of the wings flying on a hummingbird makes the infinity symbol, too.

Summary:

• Euclid wrote the first book about geometry called Elements.
• Lines can extend into infinity.
• Line segments have beginning and endings.
• Points are the places that start and/or stop line segments.
• The Plane extends into infinity.
• Lines on The Plane are either horizontal or vertical.
• The Plane is a map that shows locations of line segment points and line segments.
• Space is the area The Plane describes.