When a tutor or teacher is helping a student learn math, they will instruct the student step-by-step.  This instruction or direction is the imperative mood. The language of the math operations is used for a single math problem in the imperative mood.

The examples below are separated into one-word verbs and verbal phrases.

They are all used for one specific math problem in the sentence.

One-word Math Verbs

The first examples are the basic math operations. These words and phrases tell the student what math operation to use. This is common in beginning math classes.

Let’s look at the single words first.

add
subtract
multiply

Spoken examples are below:

“Add two plus three”
“Subtract ten minus seven”
“Multiply six times five”

The operation verbs (add, subtract, and multiply) tell the student what to do. The language for the symbols (plus, minus, or times) is used in place of the symbol.

These examples use the imperative to calculate one math problem.  Remember the language that is used for the math symbol also tells students what type of math operation to do.

Basic Math Verbal Phrases

Verbal phrases have more than one word.

Here are the math operation verbal phrases we will look at in this section:

added to
subtracted by
multiplied by
divided by

Notice that each of the verbs in the phrase end in -d or -ed suffix.  For the imperative, the bare verb is used.

For example:

“Add 2 to 3”
“Subtract 10 by 7”
“Multiply 5 by 6”
“Divide 9 by 3”

The instructional language (the imperative mood) does not use the final -ed or -d in the spelling.

Notice the words in the phrase are separated by the first number in the math operation.

These instructions could be both spoken and written for individual math problems.

Verbal Phrases for subtraction with reversed number order

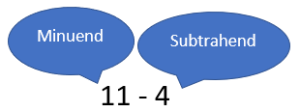
Remember with subtraction, there are phrases that reverse the order of the numbers (the minuend and subtrahend) in the math operation.

The phrases are:

subtracted from
taken from
taken away from

In the earlier chapter, we saw these phrases reverse the numbers in the operation.

First, let’s look at “subtracted from” by itself.

Remember:

• 10 – 7 can be said as, “7 subtracted from 10”.

Example of the imperative:

“subtract 7 from 10”.

Again, the final -ed is dropped.
The words of the phrasal verb are separated by the second number–the subtrahend–in the math operation.

Grammar Pause

The basic one-word verbs for math operations are regular verbs. Their suffixes will end in -d or -ed.

For example:

• add goes to added
• subtract goes to subtracted
• multiply goes to multiplied
• divide goes to divided

These regular endings are in the past participle form. This is important to know as we look at irregular verbs.

There are other verbs used in the language of math that are irregular.  Their suffixes do not use the final -d or -ed endings.

For example:

• take goes to taken (the past participle form)

As with the regular verbs, the imperative mood uses the second-person, bare verb. It does not use the past participle form.

Therefore, the imperative for the phrases “taken from” and “taken away from” are:

• take from
• take away from

The past participle suffix (-en) is dropped from the imperative mood. The phrasal verb appears in the second-person, bare verb form.

The second phrase that reverses the number order is another two-word phrase: “taken from”.

Remember,

10-7 can be said as “7 taken from 10”.

Example of the imperative:

“take 7 from 10”

The suffix is dropped and the words of the phrase are separated by the second number, again–the subtrahend–from the original math operation.

The final subtraction phrase responsible for reversing the numbers in a written subtraction problem has three-words.

• taken away from

Remember:

10 – 8    can be said as, “8 taken away from 10”
12 – 6     can be said as, “6 taken away from 12”

Examples of the imperative mood:

“take 7 away from 10”   is the imperative for 10-7
“take 1 away from 5”    is the imperative for 5-1

Yes, the verb “take” loses it’s -en suffix. The numbers in the original math operation are reversed.

Did you notice that the first and second words were separated by the number?

For example:  9 – 2

take (subtrahend number) away from (minuend number)

take 2 away from 9

It is also correct to separate the second and third words by the reversed numbers.

take away (subtrahend number) from (minuend number)

take away 2 from 9

Verbal Phrase for Division

Remember, there is a symbol that reverses the numbers for a division problem.

For example:

3⟌15

The phrasal verb for this symbol is:

3 divided into 15

The imperative for this phrasal verb is:

divide 3 into 15

And again, the two words of the phrasal verb are separated by a number in the math operation.

All of the examples in this chapter are used to talk about how to do math for a single math problem.

Summary:

• Instructions in the imperative mood can use math operation vocabulary.
• Math specific verbs and verbal phrases are used for instructions of a single math problem.